What is Dyscalculia?
To understand dyscalculia, it helps to first understand our natural quantitative abilities. We are born with an innate ability to subitize, or to see small amounts and immediately know what they are, without counting. This ability extends up to about 4 or 5 and can be thought of as our exact number system.
We are also born with an innate ability to compare larger quantities and determine which is more or less, without knowing exactly how many there are. This is known as our approximate number system.
These innate abilities are housed in specific parts of the brain, and fMRI imaging has shown that people with dyscalculia may have less activation in these areas during numerical tasks.
Brian Butterworth, a cognitive neuroscientist in the UK, has led much of the current research around dyscalculia. He describes dyscalculia as difficulty enumerating small quantities (subitizing), stemming from a core deficit in the areas of the brain responsible for processing number.
In Dyscalculia: From Science to Education, Brian Butterworth writes:
“Numbers do not seem to be meaningful for dyscalculics – at least not meaningful in the way that they are for typically developing learners. They do not intuitively grasp the size of a number and its value relative to other numbers. This basic understanding underpins all work with numbers and their relationships to one another.”
It is worth noting that this research varies from what was previously thought, which is that we are all born as blank slates (Piaget), and mathematical knowledge is primarily acquired through language. I believe this line of thought impacts math education today.
As for the word dyscalculia itself, the term was originally coined by Ladislav Kosc of Czechoslovakia in 1974, whose definition still holds true:
“Difficulty in mathematics as a result of impairment to particular parts of the brain involved in mathematical function, without a general difficulty in cognitive function.”
And getting back to basics – the first question people usually have about dyscalculia is how to say it! Dyscalculia has 5 syllables and is pronounced: dis-kal-kyoo-lee-uh. It usually takes some intentional, thoughtful practice to get it down.
For more guidance on the pronounciation, as well as the signs of dyscalculia and how it affects people in their daily lives, I recommend vising Laura Jackson’s website on Discovering Dyscalculia.
What is Effective Instruction for Dyscalculia?
The heart of effective instruction for dyscalculia is the use of dot patterns, along with Cuisenaire rods and base 10 blocks. Since dyscalculia stems from a significant weakness in the ability to subitize, the needed intervention is to develop these visual patterns in the mind’s eye, using specific dot arrangements that are easiest for the brain to visualize and transfer into long-term memory.
Research is clear that subitizing is easiest when the objects are simple (dots), the foreground and background are clearly distinguishable, and the objects are arranged into standard, ideally symmetrical, 2-dimensional arrangements with no more than 3 dots in a straight line.
Since basic or “perceptual” subitizing abilities only extend to about 4 (possibly 5 or 6 when standard arrangements are used), for larger numbers it is important to use arrangements that encourage “conceptual” subitizing, or breaking the total into 2 or more parts that are easy to subitize on their own.
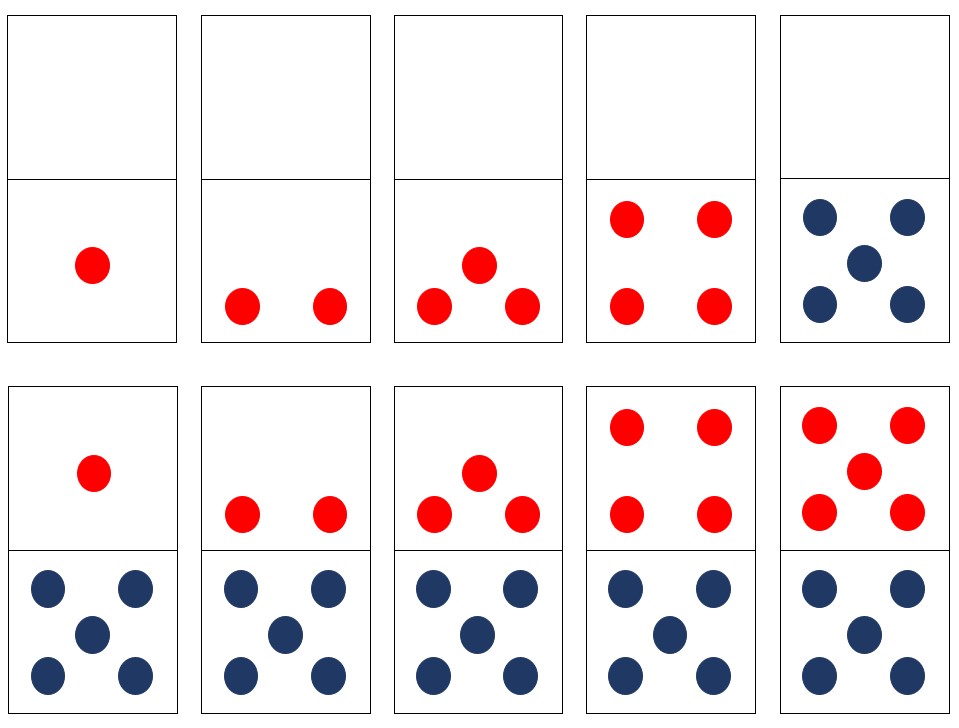
Dot Cards: 5-groups
One such example are the dot arrangements used by Chris Woodin at the Landmark School in Beverly, MA, as well as practitioners like Steve Chinn in the UK. The dots are arranged into 5-groups, with the numbers 6-10 building off the arrangements learned for 1-5. This is a powerful visual that connects to finger representations and allows students to combine 5-groups together when adding, supporting decomposition and recomposition and the all-important strategy of making 10.
Download Dot Cards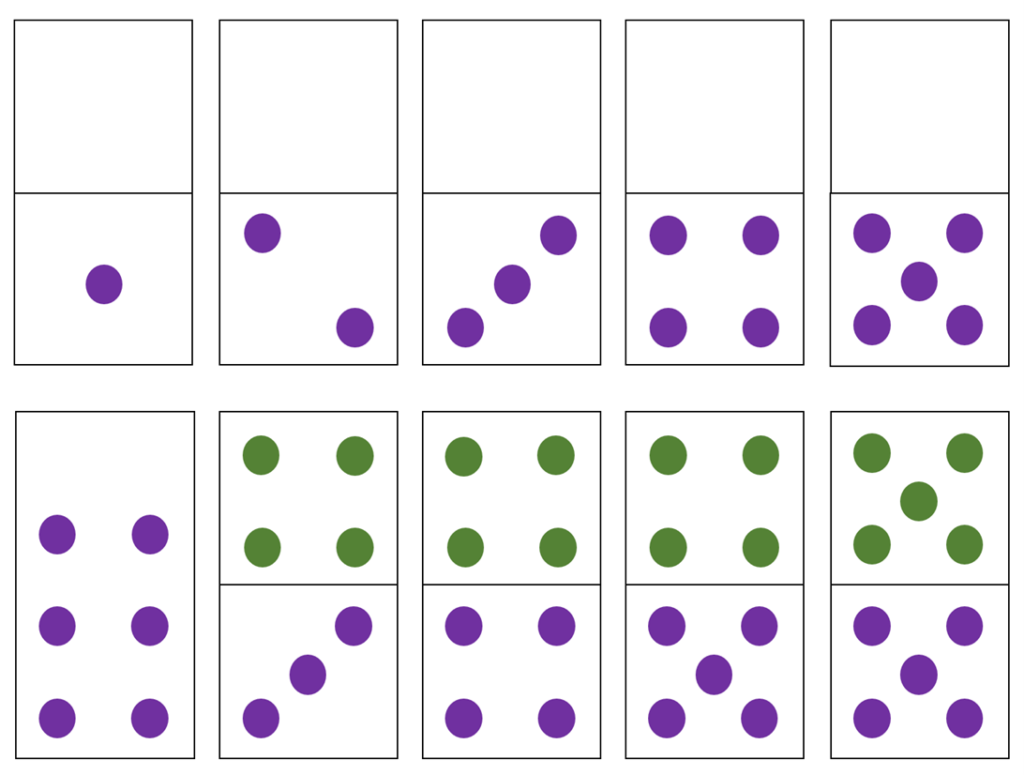
Dot Cards: Dice, Doubles, & Near Doubles
Another example are the dot arrangements used in the UK by practitioners such as Ronit Bird, Jane Emerson, and the late Dorian Yeo. The numbers 1-6 are the standard dice arrangements, and then 7-10 show the doubles or “near” doubles, facilitating the visual of whether each number is even or odd.
A variety of dot pattern cards are available on Ronit Bird’s website.
Download Dice Cards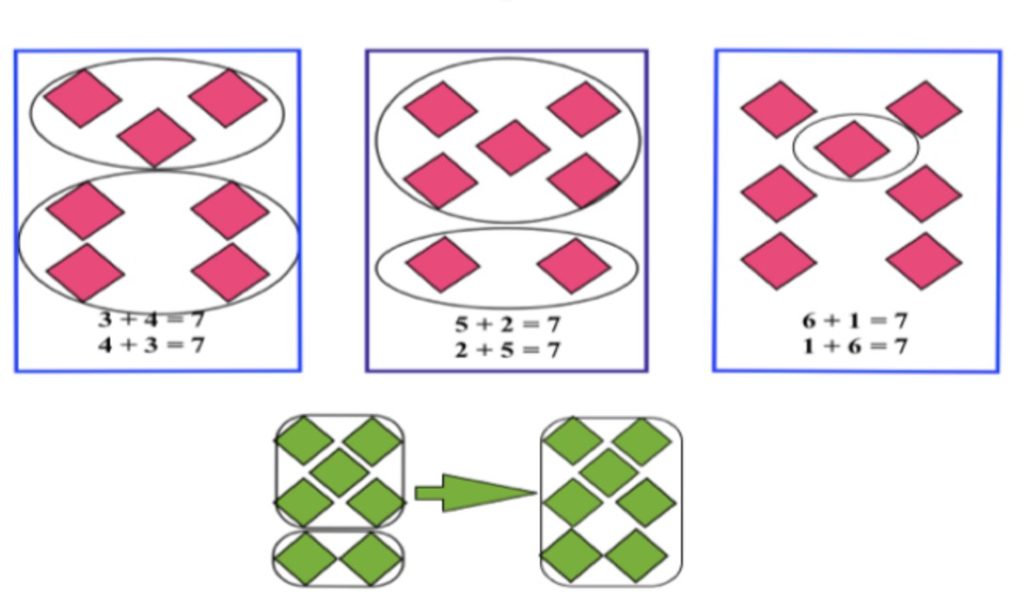
Cluster Cards
A third example is Cluster Cards as developed by Mahesh Sharma in Framingham, MA. These demonstrate a more complex visual, as the objects (“pips”) have distinct shapes of their own. The cards provide more than one arrangement for some of the numbers, integrating all of the various dot patterns, and give an opportunity for students to practice through games and generalize their learning to other environments.
Cluster Cards can be purchased by emailing Mahesh Sharma directly: [email protected]

Cuisenaire Rods
The other highly effective tool is Cuisenaire rods, which can be used along with base 10 blocks to model larger numbers. Cuisenaire rods may seem confusing at first since they are not marked by “ones” in any way that can be counted, but that is exactly why they are so effective. The color and length of each rod varies, with the number corresponding to its length in centimeters. Cuisenaire rods help students think of numbers as “chunks” of different sizes, rather than individual items to be counted. The rods support students in moving from a discrete understanding of number as individual dots to a more continuous understanding of number as length. Cuisenaire rods can be effectively used to model addition and subtraction, multiplication and division, place value, distributive property, equations, and more.
Cuisenaire rods can be purchsed from sites like Hand2Mind and Amazon. I like this individual set. For multiplication I recommend getting at least 2 sets since there are only 4 of each of the larger rods in a set.
How can I learn more?
Take the Course! Decoding Math was developed as a comprehensive course intended to introduce educators to the neuroscience of math, dyscalculia, and math learning disabilities (MLD), as well as effective instructional methods for teaching number concept, addition/subtraction, multiplication/division, word problems, and fractions/decimals/place value. The course also addresses math assessments, math-related components of IEPs, and planning math interventions.
Watch a Webinar! Interested in learning more? Watch this free recorded webinar on The Secrets of Teaching Math Facts, which gives an overview and introduction to concepts taught in the Decoding Math course.
Dyscalculia Resources
There are a growing number of resources about dyscalculia. Here are several I recommend:
- The Dyscalculia Network (UK) – on Facebook and at www.dyscalculianetwork.com
- Discovering Dyscalculia – website, blog, and book by Laura Jackson, parent of a child with dyscalculia: www.lauramjackson.com
- Brian Butterworth – Dyscalculia: From Science to Education (book) and www.mathematicalbrain.com
- Ronit Bird – The Dyscalculia Toolkit (book) and at www.ronitbird.com, as well as e-books plus videos on dot patterns and Cuisenaire rods
- The Emerson House (UK) – emerson.co.uk with Jane Emerson and books The Dyscalculia Solution and The Dyscalculia Assessment
- Mahesh Sharma – www.mathematicsforall.org
- Chris Woodin – www.woodinmath.com